Just like ProVerif, Tamarin is a protocol prover in the Dolev-Yao symbolic model. In this crypto bite, we'll have a brief look at its usage. The theoretical foundations, i.e. symbolic verification of cryptographic protocols will be covered in a separate crypto bite.

A Very Brief Summary of The Dolev-Yao Model

Before we get started with Tamarin, let's recall the Dolev-Yao model[DY83]. In that symbolic model

• all cryptographic primitives are "perfect", i.e. the adversary won't succeed to break them at all (not even with negligible probability)
• the cryptographic primitives are expressed as black boxes: we don't care about their internals and idiosyncracies. All that matters is their interactions with the protocol, and these interactions are expressed by equations. E.g.: in the symmetric encryption setting, the encryption and decryption functions are black boxes senc(m, k) and sdec(m, k). The only thing that matters is that given a key k, we can decrypt a message m encrypted by k and we'll get m back. This correctness property is expressed by the equation sdec(senc(m,k), k) = m. That's all it takes to define senc and sdec! It doesn't matter if senc and sdec is DES, 3DES, AES, ... It's a black box.
• the adversary has full control over the network: she can read, modify, intercept, drop, rearrange, and insert messages.
• proofs are a sequence of symbolic maniputations, which only take into account the equations defining the black boxes, and the rules defining the protocol. The proofs don't know anything about in internals of the black boxes.

Like ProVerif, Tamarin is a prover in the symbolic model. It is powerful and mature, and has been used among other tools to verify various drafts of the upcoming TLS 1.3 protocol[TLS13Tamarin].

Installing and Running Tamarin

Tamarin's manual shows how to download, compile, and run Tamarin [TamarinManual, Chapter 2: Installation]. On my ArchLinux-based distro Manjaro, it was as simple as running

$ sudo pacman -S tamarin-prover

which also installed the required Haskell stack, GraphViz, and Maude. The only stumbling block when starting tamarin-prover was that Maude couldn't find the file prelude.maude. To fix the issue, find that file, and set the environment variable MAUDE_LIB to point to its directory. On my system:

$ env MAUDE_LIB=/usr/share/maude tamarin-prover interactive FirstExample.spthy

We'll explore FirstExample.spthy below.

The interactive keyword causes Tamarin to start a local web server on port 3001:

$ env MAUDE_LIB=/usr/share/maude tamarin-prover interactive FirstExample.spthy 
GraphViz tool: 'dot'
 checking version: dot - graphviz version 2.40.1 (20161225.0304). OK.
maude tool: 'maude'
 checking version: 2.7.1. OK.
 checking installation: OK.
SAPIC tool: 'sapic'
Checking availablity ... OK.

The server is starting up on port 3001.
Browse to http://127.0.0.1:3001 once the server is ready.

Loading the security protocol theories './*.spthy' ...
Finished loading theories ... server ready at 

    http://127.0.0.1:3001

11/Jan/2019:18:56:29 +0100 [Info#yesod-core] Application launched @(yesod-core-1.6.9-KuG6B9OoCaHDb238Quk5RF:Yesod.Core.Dispatch ./Yesod/Core/Dispatch.hs:163:11)

Now, we're ready to start exploring that protocol:

Since I'm using Emacs, this is how to add the SPTHY main mode spthy.el: Put spthy.el into the directory ~/.emacs.d/lisp and edit the file ~/.emacs:

;; Tell emacs where personal .el files are
(add-to-list 'load-path "~/.emacs.d/lisp")

;; Load the packages (best not to include the ending ".el" or ".elc")
(load "spthy")

 That's it.

An Initial Example

To get a feeling for Tamarin, we'll show a very simple example[TamarinManual, Chapter 3: Initial Example].

An Authenticated Key Exchange Protocol

Suppose that a client \(C\) and a server \(S\) wish to establish an encrypted authenticated channel. For this, they need to agree on a symmetric key \(k\), which they could use with, e.g. AES to establish their encrypted channel. Of course, the client wants to make sure that it is indeed talking to  the intended server, and not to some adversary Eve mounting a man in the middle attack. Therefore, \(C\) and \(S\) will have to use some form of authenticated key exchange protocol (AKE). As we've seen in the series on key exchange protocols, coming up with a secure AKE protocol is tricky and very easy to get wrong. That's why we'll propose a protocol, and as a first step in its security analysis, we'll analyze it in the Dolev-Yao symbolic model. Instead of ProVerif, we'll use Tamarin here.

Like most forms of AKE, we'll assume the existence of a public key infrastructure (PKI). The server has already created a pair \((\mathit{skS}, \mathit{pkS})\) of long-term secret and public keys, and has obtained a certificate of its public key from the certificate authority CA. For simplicity, we'll write in the following \(\mathit{pkS}\) and mean both the public key and its associated certificate. The client is able to retrieve and verify \(\mathit{pkS}\) from the CA all by itself, without having to interact with \(S\).

With the PKI in place, the client and server execute the following very simple form of key exchange protocol. In simplified form, showing only the messages that get exchanged over the wire, it looks like this:

1. \(C \rightarrow S \colon \operatorname{aenc}(k, \mathit{pkS})\)
2. \(C \leftarrow S \colon h(k)\)

If we zoom in, and also show local computations performed by \(C\) and \(S\), the protocol looks like this (the actual exchange of messages is shown in blue):

1. \(C \colon k \overset{R}{\leftarrow} \{0,1\}^{\lambda}\)
2. \(C \colon k_S \leftarrow \operatorname{aenc}(k, \mathit{pkS})\)
3. \(C \rightarrow S \colon k_S\)
4. \(S \colon k' = \operatorname{adec}(k_S, \mathit{skS})\)
5. \(S \colon h_{k'} = h(k')\)
6. \(C \leftarrow S \colon h_{k'}\)
7. \(C \colon \mathit{accept} = (h(k) \overset{?}{=} h_{k'})\)

The client \(C\) starts by generating a fresh symmetric key \(k\) of \(\lambda\) random bits. In fact, we don't care about the security parameter \(\lambda\) in the symbolic model. In Tamarin code, we'll write something like Fr(~k) to generate the fresh key, without specifiying \(\lambda\) at all, but more on this later.

Next, the client retrieves and verifies the server's public key \(\mathit{pkS}\) from the CA (not shown above). Using this public key, \(C\) encrypts the ephemeral key \(k\), resulting in an encrypted key \(k_S\). Since we're in the Dolev-Yao model, we don't care about the specifics of the asymmetric encryption function used. Instead, we'll treat it as a black box and name it \(\operatorname{aenc}\). It could be RSA, EC, or whatever asymmetric encryption scheme we care about; in the symbolic model, it doesn't matter.

\(C\) then sends this encrypted key \(k_S\) to the server \(S\). Intuitively, Eve won't be able to retrieve \(k\), since \(k\) has been encrypted with \(S\)'s public key and only \(k_S\) goes over the wire.

The server will then attempt to decrypt \(k_S\) using its long-term private key \(\mathit{skS}\). To this end, it will use an asymmetric decryption function. As with encryption, we also don't care about the specifics of the decryption algorithm. We'll treat it as a black box and describe it with a function \(\operatorname{adec}\).

Whatever the key decrypts to, say, \(k'\), the server will hash with a hashing function, resulting in a hashed key \(h_{k'}\). Again, we're in the symbolic model, so we will treat the hashing function as a black box. We'll describe it with the function \(h\). The server sends the hash \(h_{k'}\) back to the client.

Finally, the client verifies that \(k = k'\) by computing \(h(k) = h_{k'} (=: h(k'))\). If the hashes match, \(C\) is persuaded that \(k\) has indeed been accepted by \(S\). Note that the security of this protocol depends crucially on the following property of the hashing function \(h\): given \(h(x)\), it should be hard for an attacker to find \(y\) such that \(h(x) = h(y)\). We call this property 2nd preimage resistance.

Is this protocol secure? If you've read the series on key exchange protocols, you'll likely say: "probably not." But if so, what exactly is wrong with it? That's what we'll try to discover, by attempting to verify it with Tamarin.

Modeling the Protocol in Tamarin

In order to submit the above KE protocol to Tamarin, we need to express it in the Tamarin language. We thus create the file FirstExample.spthy (the .spthy suffix stands for security protocol theory) in our favorite editor, and start typing:

theory FirstExample
begin

builtins: hashing, asymmetric-encryption

// ... add code here

end

We'll add code in a moment.

In the Dolev-Yao model, we reason about cryptographic primitives by treating them as black boxes. In other words, we don't care about their internal mechanisms. All we do care about are their interactions with the outside world. These interactions are described by equations. Remember the correctness property for symmetric encryption schemes, which states that every plaintext message encrypted with some key, when decrypted with the same key will yield back the original message?

\[ \forall k \in \mathcal K, \forall m \in \mathcal M \colon \operatorname{Dec}(k, \operatorname{Enc}(k, m)) = m \]

Well, that's exactly the kind of equations that provers in the symbolic model like Tamarin and ProVerif use to transform one cryptographic message into another cryptographic message. This is called equational reasoning.

Back to our FirstExample.spthy. If you recall the simple key exchange protocol above, you've noticed that we use two asymmetric functions for encryption \(\operatorname{aenc}(m, k)\) and decryption \(\operatorname{adec}(m, k)\), and a (hopefully 2nd preimage resistant) hashing function \(h(m)\). This is what the required builtins hashing and asymmetric-encryption give us. Furthermore, asymmetric-encryption also give us a unary function \(\operatorname{pk}(sk)\) which given a secret key \(\mathit{sk}\), returns the corresponding public key.

More interestingly, these builtins also define the equations we've just talked about. For example, it defines the equation

adec(aenc(m, pk(sk)), sk) = m

It says that for every message \(m\), asymmetrically encrypting it with the public key which corresponds to the recipient's secret key \(\mathit{sk}\), and then asymmetrically decrypting the resulting ciphertext with the same secret key \(\mathit{sk}\), results in the original message \(m\). This equation is indeed all it takes to model asymmetric encryption!

Instead of invoking the builtins declaration, we could just as well have written explicitely:

functions: h/1, aenc/2, adec/2, pk/1
equations: adec(aenc(m, pk(k)), k) = m

As you can see, there is nothing special about those functions. They are indeed black boxes.

Some Tamarin Syntax

To understand the code below, you need to know that Tamarin syntax uses a Perl-like syntax, where the prefix specifies the type of a variable. In particular, we have the following kinds of variables:

• ~x denotes x:fresh. Fresh variables model random numbers such a nonces and keys.
• $x denotes x:pub. A public name is known by all parties in a protocol, such as the name of a server or a client.
• #i denotes i:temporal. (... to be written: what is that?)
• m denotes m:msg. Messages are the entities that get passed along.
• 'c' denotes 'c':pub. These are public constants. They are fixed, global and known by all parties of the protocol.

The next thing to understand about Tamarin syntax is that we can state facts (just like in PROLOG) by simply inventing a relation containing variables or terms. For example, we can state that some server A has a public key pubkey simply by inventing a binary relation Pk/2 out of thin air, and stating the term Pk(A, pubkey).

At any time in the execution of the protocol, the multiset of all current facts constitutes the system's state.

The real crucial point to understand is multiset rewriting rules. A rule operates on the system's state, and when applied, it transforms the current system's state into the next system's state. So what are rules? A rule has a premise, and a conclusion. Both are separated by the arrow symbol -->.

Executing a rule requires that all facts in the premise are present in the current state and, as a result of the execution, the facts in the conclusion will be added to the state, while the premises are removed[TamarinManual]. We'll see examples below.

One more point to know are persistant facts. These can be consumed arbitrarily often, and are not removed from the system's state, even when they are stated in a premise of a rule, and that rule fires (is executed). Persistant facts are denoted by an exclamation mark prefix, e.g.: !Pk(A, pubkey). If you're from a C background, it can be hard not to unconciously misinterpret this exclamation mark as NOT. Don't.

Last, but not least, action facts: In some rules, you'll notice that the arrow --> is replaced with something like --[ ACTIONS ]->. The ACTIONS are just like normal facts (i.e. terms), but they are not part of the system's state. Instead, each time such a rule fires, the action terms are added to the "trace", which can be interpreted as a log. The trace is important, because when Tamarin reasons about some protocol, it searches the trace. We can think of actions being added to the trace as some kind of history of events that took place during the run of the protocol. An easy analogy for action facts are printf() statements that we add during debugging of a conventional program. We'll see below how action facts are used.

Modeling the Public Key Infrastructure

PKIs can be incredibly complex in the real world. But in our symbolic model for the above protocol, we need to distill the complexity of a public PKI down to a couple of symbolic rules that are relevant to our protocol. Let's see what this protocol really needs. We'll model three operations:

• registering a public key
• getting a public key
• revealing the secret key

Registerung a Public Key

An arbitrary server $A will create a fresh secret key ~ltk (short for: long term key), and will register the corresponding public key pk(~ltk) as belonging to $A with the CA. Remember that pk/1 is a builtin which is supposed to return the public key belonging to a secret key.

What does it mean to "register a public key with the CA"? Registering a public key means that we add a pair (server name, public key) to some public database. Remember the system's state? This is a database of all known facts at a specific time (if you know PROLOG, you'll know what I'm talking about). This database contains terms (facts) and grows each time a rule which adds to that database fires. So this is an ideal place to insert/append that pair.

There's a slight catch though: a pair is not strongly typed: we could have more pairs in the system state with totally different meanings. So, what do we do?

What kind of term could we use to represent the fact that a public key belongs to a specific server? Well, we simply invent (out of thin air) a binary relation Pk/2 (note: capital P), and we'll denote by Pk($A, pk(~ltk)) the fact that the public key associated with the freshly generated secret key ~ltk belongs to server name $A. This fact we could simply append to the system state.

Is that all we need to register? It could be. But we want to get more fancy, and we want also register the fact that ~ltk is the long term key (secret key) belonging to server $A. This begs the question: why would we want to do this? Below, we'll want to explore the consequences of the secret key ~ltk being compromized. Because there are many possible servers, we want Tamarin to be able to trace back a specific ~ltk to the server $A that created it. That's why we need to record that fact in the system state too. How do we do this? Exactly as we did with the public key association Pk/2! We invent (again out of thin air) another relation Ltk/2, and we'll record the term Ltk($A, ~ltk) in the system state at keypair creation time.

We therefore add the following rule to FirstExample.spthy:

// Registering a public key
rule Register_pk:
    [ Fr(~ltk) ]
  -->
    [ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]

If you recall the way rules work: the rule fires if and only if the facts in the condition (before the arrow -->) are present in the system's state. After firing, those facts are removed from the system's state, and the facts in the conclusion (after the arrow) are added to the system's state.

When the fresh variable ~ltk is being generated the first time, Tamarin adds the fact Fr(~ltk) to its system state. The builtin Fr fact denotes a freshly generated name. Therefore, the condition is satisfied and the rule Register_pk fires. This means that Fr(~ltk) is then removed from the system state (well, it is not freshly generated anymore).

Then, the two terms in the conclusion, Ltk($A, ~ltk) and Pk($A, pk(~ltk)) are added to the system state. We therefore recorded both the (server name, public key), and the (server name, secret key) associations in the global database.

What's the business with the dollar prefix in $A? It means that Tamarin choses non-deterministically a new public name A for the server that is generating the key pair. Think of the generated name to be something like A0324.

Why did we prefix the Ltk/2 and Pk/2 terms with an exclamation mark? We want those facts to be persistent. In other words: even if we specify those facts in the condition of a rule, we don't want them to disappear (as non-persistent facts would) when that rule fires.

Getting the Public Key

Generating and registering a public key in the system state would be pointless if we couldn't read it back. What do we want to model here? (server name, public key) associations are meant to be publicly accessible by anyone (including by the adversary). We will simply write a rule Get_pk, which says that if some (persistent) association !Pk(A, pubkey) for some server name A exists in the system state, then pubkey should be output on the common channel. The rule looks like this:

rule Get_pk:
    [ !Pk(A, pubkey) ]
  -->
    [ Out(pubkey) ]

There are two implicit assumptions here that we need to be aware of:

• Searches in the database are implicit. As usual with Haskell and other languages of the ML family, pattern matching (or rather a more general form called unification) is automatically applied to match, say, the registered fact !Pk("hajji.org", "mypubkey") in the database with the term !Pk(A, pubkey) from the rule. In this case, pattern matching succeeds, because both term names !Pk/2 match, and the subterms A is then matched with "hajji.org" (so A becomes instantiated with that string), and pubkey becomes instantiated with my "mypubkey". Actually, it is not exactly like this (terms are passed around, not (bit-)strings), but this is a good enough analogy it you come from the Haskell or ML world.
• By default, Tamarin assumes that all actors, including the adversary, are connected to a common broadcast channel. Out(pubkey) denotes the fact that the term pubkey is being sent (output) to that channel. Therefore, all actors become aware of pubkey at this point. Other network topologies can be modeled by Tamarin, but for now, this common broadcast channel is sufficient.

Revealing the Secret Key

Just like fetching the (server name, public key) association from the system state with the rule Get_pk, we'll add a rule Reveal_ltk which will fetch the (server name, secret key) from the system state, and broadcast that secret key on the common channel. This models a security breach into server "server name" where e.g. a hacker managed to exfiltrate that server's secret key:

rule Reveal_ltk:
    [ !Ltk(A, ltk) ]
  --[ LtkReveal(A) ]->
    [ Out(ltk) ]

I won't repeat how the !Ltk(A, ltk) fact is being searched through pattern matching in the system state.

What's more interesting ist that now, we also have an action fact: LtkReveal(A). Recall that action facts are the equivalent of printf() debug statements in conventional programming. Each time this rule Reveal_ltk fires, the fact LtkReveal(A) will be added to the "trace", a global list of events that Tamarin uses to reason. Actually, the whole point of modeling the PKI this way is to generate this action fact. We'll see why below.

What is LtkReveal(A)? First of all, it is a unary relation LtkReveal/1 that we invented again out of thin air to denote the fact, that there was a breach of secret key with a named server. Which server? Well, the one whose name A was instantiated to in the condition !Ltk(A, ltk). It is important to note that in a multi-server setup, there can be many different servers, each with its different name (symbol), think something like A00324, A34234, A93412, ... We want the trace to identity the specific server that suffered the breach of its secret key.

You may wonder why we wrote ltk instead of ~ltk. The reason ist this: when pattern-matching the condition !Ltk(A, ltk), we want the variable ltk to be instantiated to whatever was recorded in that term in the system state. This will typically be our ~ltk for our $A.

By the same token, A will be instantiated with our $A. But let's not dwell on that.

Now, we're done modeling the PKI. Time to model the protocol itself.

Modeling the Protocol

First, recall the protocol:

• \(C \rightarrow S \colon \operatorname{aenc}(k, \mathit{pkS})\)
• \(C \leftarrow S \colon h(k)\)

Let's start with the client. C runs two times. The first time it generates the session key, encrypts it with the public key of the server, and then sends the result via the broadcast channel to the server. The second time, the clients receives the reply from the server, and if that reply is indeed well-formed (i.e. if it is the hash of the session key), it logs the session key in the trace.

We could model both runs of the client with two rules Client_1 and Client_2:

// Start a new thread executing the client role, choosing the server
// non-deterministically.
rule Client_1:
    [ Fr(~k)         // choose fresh key
    , !Pk($S, pkS)   // lookup public-key of server
    ]
  -->
    [ Client_1( $S, ~k )    // Store server and key for next step of thread
    , Out( aenc(~k, pkS) )  // Send the encrypted session key to the server
    ]

rule Client_2:
    [ Client_1(S, k)   // Retrieve server and session key from previous step
    , In( h(k) )       // Receive hashed session key from network
    ]
  --[ SessKeyC( S, k ) ]-> // State that the session key 'k'
    []                     // was setup with server 'S'

By now, you should be able to read these rules quite easily (but see below for a quick explainer if you're unsure).

The interesting part is that the client needs to store the session key ~k and the selected server $S (actually the association between both) at the end of the first rule, so that it can pick it up in the second rule. But where do we save that state between both rules? Well, in the system state, of course. For this, we invent again a binary relation Client_1/2 (out of this air -- I love this expression, don't I?), and by stating the term Client_1($S, ~k) in the conclusion of the Client_1 rule, we store it as usual in the system state. Next, in the Client_2 rule, we read that state back by looking up the Client_1/2 fact, thereby re-instantiating the corresponding server name $S and session key ~k.

You may be confused here: both the rule Client_1 and the binary relation Client_1/2 seem to have the same name. But both are totally different symbols. For one, Client_1 is a rule, and Client_1/2 is a relation. We could have used any other name for the relation, like, say, State_Client/2 or whatever, so long as we remain consistent when reading it back in the Client_2 rule. Using the same name for the rule and the state is a convenient convention, as it allows us to chain many rules together.

A little explainer: All starts with the rule Client_1. But why does it get invoked at all? At first, since the fresh key ~k is still fresh, the builtin fact Fr(~k) holds. Furthermore, some server will have registered a public key with the rule Register_pk (see above), and would therefore have added the fact !Pk($S, pkS) to the system state, for some name S. So both conditions for rule Client_1 are met, and that rule fires.

As a result, the client stores the intermediate state Client_1($S, ~k) on the system state, encrypts ~k with the corresponding public key of the selected server, and sends this out on the common communication channel by stating Out(aenc(~k, pkS))

When the server responds, the second rule Client_2 fires, because its conditions are satisfied: the state is still there, and now, reading from the communications channel with the builtin In() succeeds. But hold on: where does the client verify that it got the hash of the session key that it sent to the server? Remember pattern matching? The condition In(h(k)) pattern matches only if what was read via In() is a hash of the session key that was retrieved from the previously saved state. If someone sent the hash of a wong key, say k', h(k) wouldn't pattern match h(k'), and therefore, the rule Client_2 wouldn't fire. And if someone used a different function to hash, say h'(), then there wouldn't be a match either.

Exercise: Does the fact that h(k) and h(k') can't pattern match when k and k' are different capture the notion "2nd preimage resistance" of the hash function h/1?

What Client_2 really does is to record an action fact SessKeyC(S, k) on the trace. This logs the fact that the client successfully established a session key k with server name S. This will be important further down, when we state desired security properties that we want Tamarin to prove or disprove for us.

Now, on to the server. The rule governing the server's behaviour is much simpler.  Since the server doen't need to be activated twice, one rule suffices, as the server doesn't have to temporarily store some state while waiting for a reply:

// A server thread answering in one-step to a session-key setup request from
// some client.
rule Serv_1:
    [ !Ltk($S, ~ltkS)                             // lookup the private-key
    , In( request )                               // receive a request
    ]
  --[ AnswerRequest($S, adec(request, ~ltkS)) ]-> // Explanation below
    [ Out( h(adec(request, ~ltkS)) ) ]            // Return the hash of the
                                                  // decrypted request.

Does the rule Serv_1 fire at all? Let's see. The persistent fact !Ltk($S, ~ltkS) was recorded in the system state by the rule Register_pk, which itself fired because ~ltk was fresh to begin with. Furthermore, the fact In(request) holds the instant that someone wrote something on the communication channel with Out(). Since Client_1 fired too, and wrote something with Out(), the variable request will instantiate to that something, i.e. to aenc(~k, pkS).

Since Serv_1 fires, two things happen: the conclusion facts are stored in the system state, and the action fact will be stored in the trace. The conclusion facts consist of the simple fact Out(h(adec(request, ~ltkS))). Therefore, the server writes the hash of the decrypted request (decrypting using its own secret key ~ltkS it got from the system state) to the communications channel... where it will hopefully be read by the Client_2 rule. More important: the server logs the action fact AnswerRequest($S, adec(request, ~ltkS)) in the trace, so Tamarin can use it to prove or disprove the desired security properties to be shown below. AnswerRequest/2 simply states that server $S was able to decrypt request with its secret key ~ltkS (and that it will send the hashed value of that decryption back).

If you come to think of it, this protocol specification is quite natural. This is because it uses a combination of pattern matching and of π-calculus.

Specifying the Desired Security Properties (Lemmata)

Security properties are defined over traces of the action facts of a protocol execution[TamarinManual, Modeling security properties].

What action facts could possibly be in the trace?

• SessKeyC(S, k): the client successfully established a session key k with server S. This means that it got h(k), the hash of k, back from the communication channel, hopefully from the server S.
• AnswerRequest(S, adec(request, ltk)): the server S successfully decrypted this request it got from the communication channel with its own secret key ltk, and will therefore send the hash of this decrypted request out on the communication channel, where it will be hopefully picked up by the client.
• LtkReveal(S): the long-term (secret) key of server S has been compromized.

In any case, whatever is being sent out of the communication channel with Out() can also be read by an adversary. Furthermore, the adversary may inject messages into the communication channel where they will be picked up by anyone that performs an In(). This Dolev-Yao adversary has even more capabilites.

One scary capability that the adversary has, is to hack into some server S and expose its long term (secret) key. It does this when it invokes the rule Reveal_ltk that we've introduced when modelling the PKI.

Anyway... For this simple protocol, we now want to prove (or disprove) the following arbitrary properties, which exculsively use those action facts that were recorded in the trace:

• Secrecy of session key from the client perspective: If a client has set up a session key k with a server S (i.e. if the action fact SessKeyC(S, k) has been recorded in the trace), and the adversary knows k, then this can only happen it the long term (secret) key of server S has been compromized (i.e. it the action fact LtkReveal(S) has been recorded in the trace).
• Client authentication: If a client has set up a session key k with server S (that is if SessKeyC(S, k) has been recorded), then it must be that server S answered that request (i.e. that AnswerRequest(S, k) has been recorded), or that the adversary compromized the long term key of S (meaning that LtkReveal(S) has been recorded) before the client has set up this session key k
• Injective authentication: This is a strengthened version of client authentication, which requires that no other client sent the same request: If a client has set up a session key k with server S (again, that SessKeyC(S, k) has been recorded), then there must be a server S that answered that request (that AnswerRequest(S, k) has been recorded) and that no other client has sent the same request (that SessKeyC(S, k) hasn't been recorded twice in the system state), or that the adversary compromized the secret key of S (that LtkReveal(S) has been recorded) before the key was setup.

So how do we express this in Tamarin? Secrecy of session key from the client perspective is expressed by the following lemma:

lemma Client_session_key_secrecy:
  " /* It cannot be that a  */
    not(
      Ex S k #i #j.
        /* client has set up a session key 'k' with a server'S' */
        SessKeyC(S, k) @ #i
        /* and the adversary knows 'k' */
      & K(k) @ #j
        /* without having performed a long-term key reveal on 'S'. */
      & not(Ex #r. LtkReveal(S) @ r)
    )
  "

The first thing to note is the use of quantifiers (here Ex). The second point is the use of temporal variables (here #i and #j). We can imagine these as some kind of line numbers in the trace, i.e. a time stamp of the recorded action facts. Finally, the fact K(k) stands for: the adversary knows k. We didn't define it explicitely; it is a builtin fact that consumes Out(), i.e. everything that goes over the wire, the adversary automatically knows (which makes sense).

Client authentication is expressed like this:

lemma Client_auth:
  " /* For all session keys 'k' setup by clients with a server 'S' */
    ( All S k #i.  SessKeyC(S, k) @ #i
       ==>
         /* there is a server that answered the request */
       ( (Ex #a. AnswerRequest(S, k) @ a)
         /* or the adversary performed a long-term key reveal on 'S'
            before the key was setup. */
       | (Ex #r. LtkReveal(S) @ r & r < i)
       )
    )
  "

Again, note the use of quantifiers (All and Ex). Interesting also is the use of an implication denoted by ==>. Finally, note how we can express that one event took place before another, by comparing the temporal variables r und i.

The strengthtened version of client authentication:

lemma Client_auth_injective:
  " /* For all session keys 'k' setup by clients with a server 'S' */
    ( All S k #i.  SessKeyC(S, k) @ #i
       ==>
         /* there is a server that answered the request */
       ( (Ex #a. AnswerRequest(S, k) @ a
           /* and there is no other client that had the same request */
           & (All #j. SessKeyC(S, k) @ #j ==> #i = #j)
       )
         /* or the adversary performed a long-term key reveal on 'S'
            before the key was setup. */
       | (Ex #r. LtkReveal(S) @ r & r < i)
       )
    )
  "

By now, you should be able to decipher this lemma notation all by yourself. The only stumbling block is the equality operator between the temporal variables #i and #j: the model assumes that all client threads run simultaneously, and therefore record their SessKeyC(S, k) action fact with the same timestamp in the system log.

(... to do: explain bootstrapping)

And finally, the bootstrapping property:

lemma Client_session_key_honest_setup:
  exists-trace
  " Ex S k #i.
        SessKeyC(S, k) @ #i
      & not(Ex #r. LtkReveal(S) @ r)
  "

(... to be written)

Tamarin Worflow

We can now try to prove or disprove these lemmata with Tamarin. Since such proofs don't always terminate, it may be necessary to guide Tamarin by manually selecting the desired proof strategy, and by selecting the next goal that is to be proven. Therefore, the following workflow is typical for Tamarin usage:

Checking the well-formedness of the theory

We first call tamarin-prover with the file FirstExample.spthy to check for syntax errors and well-formedness of the theory. This will also pretty-print the theory:

$ env MAUDE_LIB=/usr/share/maude tamarin-prover FirstExample.spthy
maude tool: 'maude'
 checking version: 2.7.1. OK.
 checking installation: OK.
SAPIC tool: 'sapic'
Checking availablity ... OK.

theory FirstExample begin

// Function signature and definition of the equational theory E

functions: adec/2, aenc/2, fst/1, h/1, pair/2, pk/1, snd/1
equations:
    adec(aenc(x.1, pk(x.2)), x.2) = x.1,
    fst(<x.1, x.2>) = x.1,
    snd(<x.1, x.2>) = x.2

rule (modulo E) Register_pk:
   [ Fr( ~ltk ) ] --> [ !Ltk( $A, ~ltk ), !Pk( $A, pk(~ltk) ) ]

  /* has exactly the trivial AC variant */

rule (modulo E) Get_pk:
   [ !Pk( A, pubkey ) ] --> [ Out( pubkey ) ]

  /* has exactly the trivial AC variant */

rule (modulo E) Reveal_ltk:
   [ !Ltk( A, ltk ) ] --[ LtkReveal( A ) ]-> [ Out( ltk ) ]

  /* has exactly the trivial AC variant */

rule (modulo E) Client_1:
   [ Fr( ~k ), !Pk( $S, pkS ) ]
  -->
   [ Client_1( $S, ~k ), Out( aenc(~k, pkS) ) ]

  /* has exactly the trivial AC variant */

rule (modulo E) Client_2:
   [ Client_1( S, k ), In( h(k) ) ] --[ SessKeyC( S, k ) ]-> [ ]

  /* has exactly the trivial AC variant */

rule (modulo E) Serv_1:
   [ !Ltk( $S, ~ltkS ), In( request ) ]
  --[ AnswerRequest( $S, adec(request, ~ltkS) ) ]->
   [ Out( h(adec(request, ~ltkS)) ) ]

  /*
  rule (modulo AC) Serv_1:
     [ !Ltk( $S, ~ltkS ), In( request ) ]
    --[ AnswerRequest( $S, z ) ]->
     [ Out( h(z) ) ]
    variants (modulo AC)
    1. ~ltkS = ~ltkS.5
       request
             = request.5
       z     = adec(request.5, ~ltkS.5)
    
    2. ~ltkS = ~x.5
       request
             = aenc(x.6, pk(~x.5))
       z     = x.6
  */

lemma Client_session_key_secrecy:
  all-traces
  "¬(∃ S k #i #j.
      ((SessKeyC( S, k ) @ #i) ∧ (K( k ) @ #j)) ∧
      (¬(∃ #r. LtkReveal( S ) @ #r)))"
/*
guarded formula characterizing all counter-examples:
"∃ S k #i #j.
  (SessKeyC( S, k ) @ #i) ∧ (K( k ) @ #j)
 ∧
  ∀ #r. (LtkReveal( S ) @ #r) ⇒ ⊥"
*/
by sorry

lemma Client_auth:
  all-traces
  "∀ S k #i.
    (SessKeyC( S, k ) @ #i) ⇒
    ((∃ #a. AnswerRequest( S, k ) @ #a) ∨
     (∃ #r. (LtkReveal( S ) @ #r) ∧ (#r < #i)))"
/*
guarded formula characterizing all counter-examples:
"∃ S k #i.
  (SessKeyC( S, k ) @ #i)
 ∧
  (∀ #a. (AnswerRequest( S, k ) @ #a) ⇒ ⊥) ∧
  (∀ #r. (LtkReveal( S ) @ #r) ⇒ ¬(#r < #i))"
*/
by sorry

lemma Client_auth_injective:
  all-traces
  "∀ S k #i.
    (SessKeyC( S, k ) @ #i) ⇒
    ((∃ #a.
       (AnswerRequest( S, k ) @ #a) ∧
       (∀ #j. (SessKeyC( S, k ) @ #j) ⇒ (#i = #j))) ∨
     (∃ #r. (LtkReveal( S ) @ #r) ∧ (#r < #i)))"
/*
guarded formula characterizing all counter-examples:
"∃ S k #i.
  (SessKeyC( S, k ) @ #i)
 ∧
  (∀ #a.
    (AnswerRequest( S, k ) @ #a)
   ⇒
    ∃ #j. (SessKeyC( S, k ) @ #j) ∧ ¬(#i = #j)) ∧
  (∀ #r. (LtkReveal( S ) @ #r) ⇒ ¬(#r < #i))"
*/
by sorry

lemma Client_session_key_honest_setup:
  exists-trace
  "∃ S k #i. (SessKeyC( S, k ) @ #i) ∧ (¬(∃ #r. LtkReveal( S ) @ #r))"
/*
guarded formula characterizing all satisfying traces:
"∃ S k #i. (SessKeyC( S, k ) @ #i) ∧ ∀ #r. (LtkReveal( S ) @ #r) ⇒ ⊥"
*/
by sorry

/* All well-formedness checks were successful. */

end

==============================================================================
summary of summaries:

analyzed: FirstExample.spthy

  Client_session_key_secrecy (all-traces): analysis incomplete (1 steps)
  Client_auth (all-traces): analysis incomplete (1 steps)
  Client_auth_injective (all-traces): analysis incomplete (1 steps)
  Client_session_key_honest_setup (exists-trace): analysis incomplete (1 steps)

==============================================================================

We see that no errors or warnings were reported. Missing a warning is not a good idea. Use --quit-on-warning if needed.

Anyway, at this point, we didn't run any proofs yet.

Running All Proofs Automatically

If we always select the first proof stratagy, and all those proofs terminate, we could just as well run them non-interactively from the command line:

$ env MAUDE_LIB=/usr/share/maude tamarin-prover FirstExample.spthy --prove

(... long output followed by)

==============================================================================
summary of summaries:

analyzed: FirstExample.spthy

  Client_session_key_secrecy (all-traces): verified (5 steps)
  Client_auth (all-traces): verified (11 steps)
  Client_auth_injective (all-traces): verified (15 steps)
  Client_session_key_honest_setup (exists-trace): verified (5 steps)

==============================================================================

As we can see, all lemmata were proven correct!

To prove only one lemma, specify it as argument to --prove, e.g.:

$ env MAUDE_LIB=/usr/share/maude tamarin-prover FirstExample.spthy --prove=Client_session_key_secrecy
maude tool: 'maude'
 checking version: 2.7.1. OK.
 checking installation: OK.
SAPIC tool: 'sapic'
Checking availablity ... OK.

  solved goal nr. 0 (directly): SessKeyC( S, k.1 ) @ #i.2
  solved goal nr. 1 (directly): K( k.1 ) @ #j.3
  solved goal nr. 0 (directly): !Ltk( t.1, t.2 ) ▶₀ #i
  solved goal nr. 0 (directly): !Pk( t.1, t.2 ) ▶₀ #i
  solved goal nr. 0 (directly): Client_1( t.1, t.2 ) ▶₀ #i
  solved goal nr. 0 (directly): !KU( pk(t.1) ) @ #i
  solved goal nr. 0 (directly): !KU( fst(t.1) ) @ #i
  solved goal nr. 0 (directly): !KU( h(t.1) ) @ #i
  solved goal nr. 0 (directly): !KU( aenc(t.1, t.2) ) @ #i
  solved goal nr. 0 (directly): !KU( ~t.1 ) @ #i
  solved goal nr. 0 (directly): !KU( adec(t.1, t.2) ) @ #i
  solved goal nr. 0 (directly): !KU( snd(t.1) ) @ #i
  solved goal nr. 2 (directly): !Pk( $S.4, pkS.4 ) ▶₁ #vr.3
  solved goal nr. 4 (directly): !Pk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Pk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Pk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Pk( A.10, t.8 ) ▶₀ #vr.9
  solved goal nr. 4 (directly): !Pk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Pk( A.10, t.8 ) ▶₀ #vr.9
  solved goal nr. 4 (directly): !Pk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Ltk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Ltk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Ltk( A.10, t.8 ) ▶₀ #vr.9
  solved goal nr. 4 (directly): !Ltk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Ltk( A.10, t.8 ) ▶₀ #vr.9
  solved goal nr. 4 (directly): !Ltk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Ltk( A.7, t.5 ) ▶₀ #vr.6
  solved goal nr. 4 (directly): !Pk( $S.10, t.2 ) ▶₁ #vr.9
  solved goal nr. 4 (directly): !Pk( $S.7, pk(x.11) ) ▶₁ #vr.6
  solved goal nr. 4 (directly): !Ltk( $S.7, ~ltkS.7 ) ▶₀ #vr.6
  solved goal nr. 3 (precomputed): Client_1( S, k ) ▶₀ #i
  solved goal nr. 9 (precomputed): !KU( ~k ) @ #vk.1
  solved goal nr. 11 (precomputed): !KU( ~ltk ) @ #vk.2

(... pretty print of the theory elided)

/* All well-formedness checks were successful. */

end

==============================================================================
summary of summaries:

analyzed: FirstExample.spthy

  Client_session_key_secrecy (all-traces): verified (5 steps)
  Client_auth (all-traces): analysis incomplete (1 steps)
  Client_auth_injective (all-traces): analysis incomplete (1 steps)
  Client_session_key_honest_setup (exists-trace): analysis incomplete (1 steps)

==============================================================================

Tamarin pretty-printed the theory again, but now, it also listed the goals to be proven. These goals, Tamarin derived itself from the theory. To understand the goals, all you need to know at this point is that K/1, KU/1 and KD/1 denote what the adversary knows. The remaining goals should be obvious by now.

Exploring Verifications Interactively

Every now and then, a proof may be stuck in an infinite loop, i.e. it doesn't terminate. If this happens, we need to manually guide Tamarin by selecting one of many proof heuristics, or by selecting the next goal to be proven. By doing this, we avoid the non-terminating branches of the search tree. This is akin to placing cuts in PROLOG programs to prune the search tree.

Running proofs interactively means that we will use the browser. We've already started Tamarin's web server above. In order not to miss warnings (which happens easily), we also add the flag --quit-on-warning:

$ env MAUDE_LIB=/usr/share/maude tamarin-prover interactive FirstExample.spthy --quit-on-warning

Now, in the browser, click on "FirstExample":

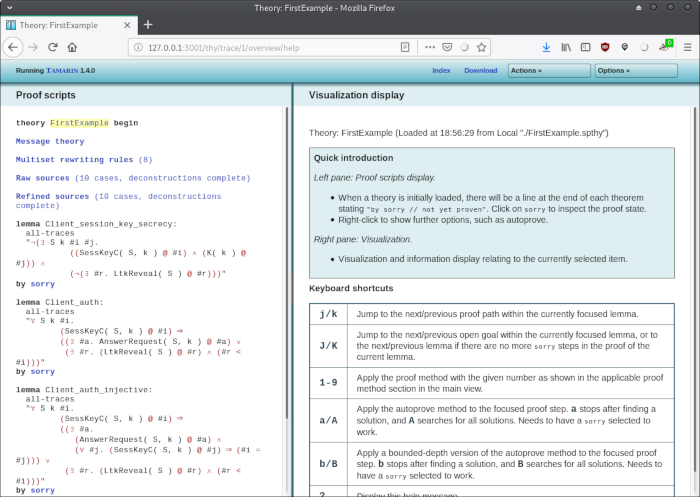
We see the lemmata on the left, and a visualization display on the right. By clicking on the "sorry" link below a lemma, we will start a proof for that lemma. But before doing this, let's frist look around a litte bit. Click on "Message theory":

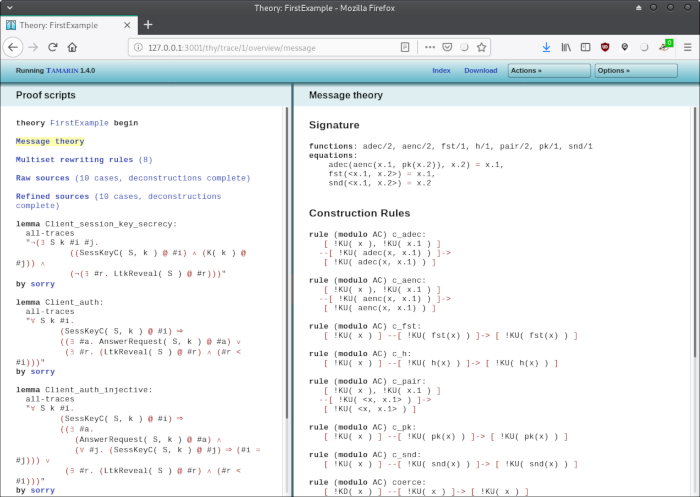
Let's look at the "Multiset rewriting rules (8)" link:

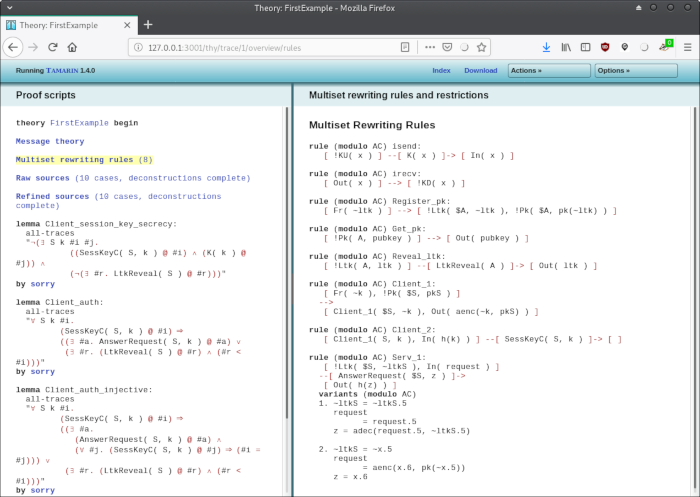
More interesting is the "Raw Sources (10 cases, deconstructions complete)" screen:

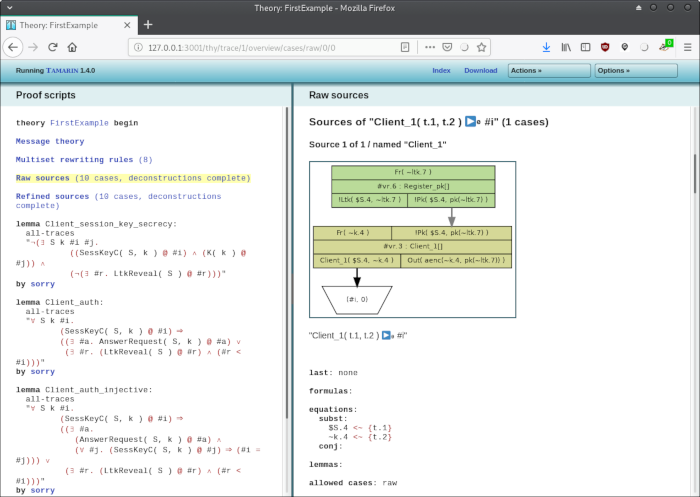
Sources tell us what series of rule firings cased a fact to be written in the system state. Let's consider the fact Client_1( t.1, t.2 ) that was the state saved by Client_1 before it can be picked up by Client_2. What sequence of rule invocations caused it to be added to the system state? Let's see!

We scroll down to Client_1( t.1, t.2 ) as shown in the screenshot above. Here, t.1 and t.2 are just placeholders. The green boxes display rule invocations by showing the conditions at the top, the name of the fired rule and the instance that fired it in the middle, and the conclusions at the bottom.

We interpret this picture from the bottom to the top, going in the inverse direction of the arrows. The trapeze is a sink, which we don't care about. What's more interesting is that the fact Client_1($S.4, ~k.4) was part of the conclusions of an invocation of the Client_1 rule, as can be seen by looking at the middle green box.

But what caused that rule to be fired? Going up to the upper box, we see that the condition !Pk($4, pk(~ltk.7)) was added to the system state by in invocation of the rule Register_pk, which itself was fired because its condition Fr(~ltk.7) was fulfilled by default. Of course, the other condition Fr(~k.4) of the Client_1 rule was also defined by default.

In other words: Client_1 was fired, because some server registered its public key by invoking the rule Register_pk.

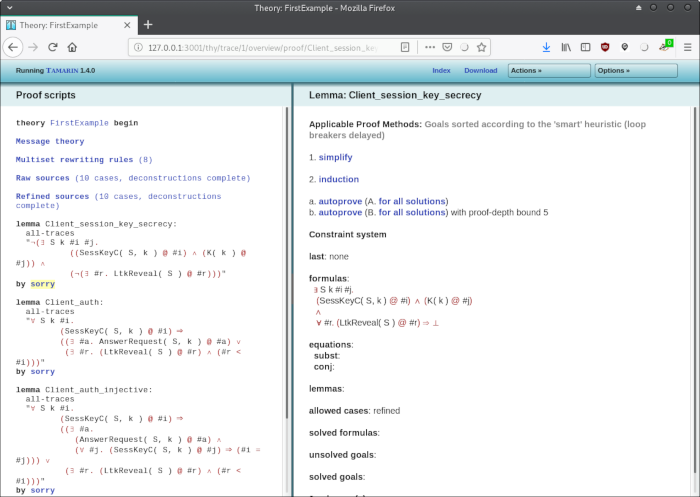
Now, let't try to prove the first lemma. Click on "sorry" at the bottom the lemma Client_session_key_secrecy. We get an overview screen with various proof strategies:

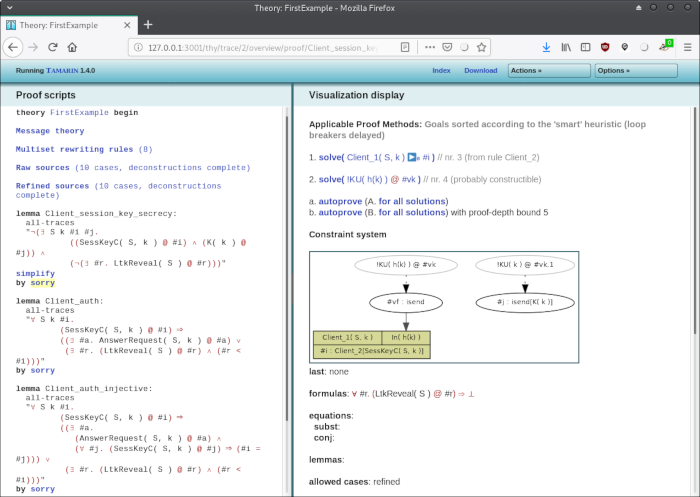
This is the point were we can manually select various proof strategies. We go with "simplify":

(... to do: explain this screen)

There are two goals to solve. We go here with the first one by clicking on 1. solve (Client_1 ..):

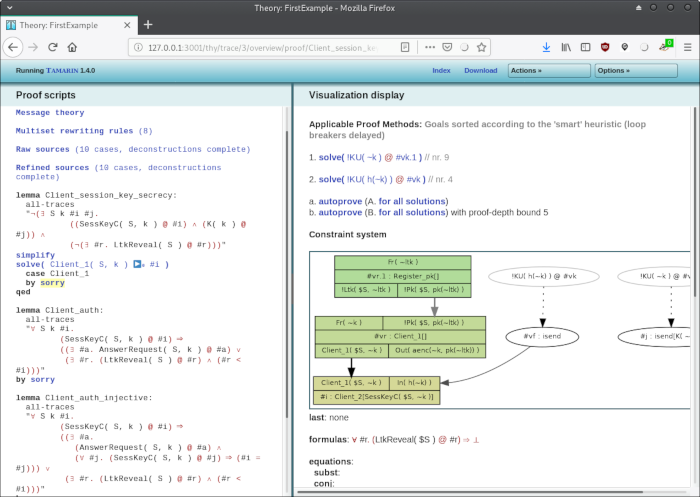
(... to do: explain this screen)

Again, we can manually chose which of the two goals to solve. We go once more with the first one:

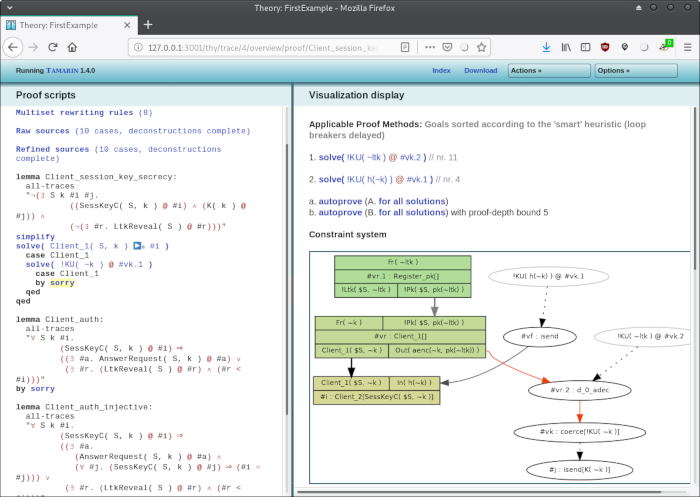
(... to do: explain this screen)

And one last time, we manually select the first goal. Note that if we always select the first goal, this is exactly what "autoprove" does. There is also a version of "autoprove" that stops at 5 steps, which is useful it we encounter a non-terminating branch. Anyway, clicking on the first goal again, we get this screenshot:

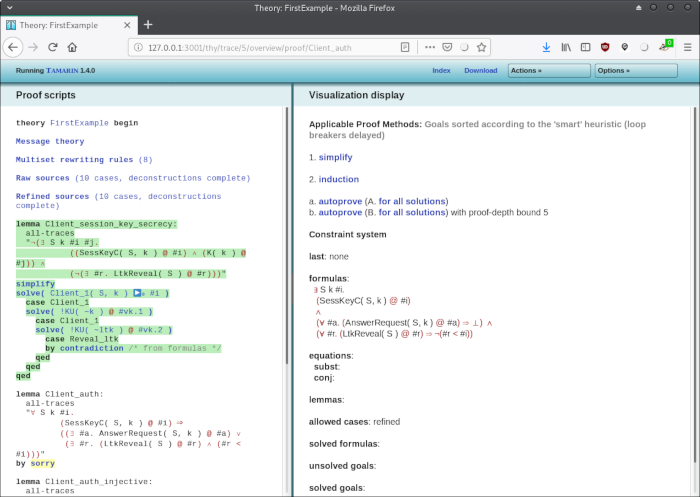
The lemma turned green, which means that it was successfully proved.

If the proof didn't get through, the lemma would have turned red, and a counter-example would have been displayed.

Summary

Let's summarize what we've learned so far:

• Tamarin is a prover in the symbolic model, where cryptographic primitives are modeled as black boxes.
• Protocols are modeled with multiset rewriting rules, where the premises (conditions) are removed from and conclusions are added to the system state when a rule fires
• Interesting events during the protocol execution are modeled as action facts. They are added to the "trace" when encountered (when a rule fires).
• The required security properties are stated as lemmas, which Tamarin tries to prove.
• The properties define conditions on the action facts in the trace. That's why action facts are pivotal in Tamarin.
• There is a batch mode where Tamarin attempts to prove all lemmata, but this mode can fail when a proof doesn't terminate.
• In this case, one can also run Tamarin in interactive mode, and the user can manually guide the proof by selecting proof strategies and the next goal to prove at each step.
• If Tamarin manges to prove a lemma, that lemma turns green; if it can disprove it, the lemma turns red and a counter-example shows up.
• Only the lemmata that we wrote can be proven (or disproven); Tamarin doesn't invent lemmata on its own
• In some dark cases (when e.g. the finite variant property is not met, see [TamarinManual, Equational Theories]) a proof can silently fail without reason.

The next steps in your journey into Tamarin would be

• to watch the demo at the end of this crypto bite to see a counter example,
• to read the Tamarin manual [TamarinManual]
• to look at various example protocols in the Tamarin distribution,
• and to see how TLS 1.3 is being verified with Tamarin [TLS13Tamarin].
• You may also want to learn about the theoretical foundations of Tamarin by studying [Schmidt12, Meier13]

The take away from this is that Tamarin doesn't prove that a protocol is secure. It rather helps verifying whether certain security properties (lemmata) hold. It is the responsibility of the user to identify those security properties! Experience with protocol analysis is key here, as is with various kinds of attacks on the logical flaws of cryptographic protocols. In other words: Tamarin is a proof assistant, it is not a panacea.

Furthermore, once logical protocol flaws have been weeded out of a protocol, there is still the need to analyze it in the computational model, i.e. with real crypto proofs. Tools like CryptoVerif come in handy at this next step.

Sources

The initial example is taken verbatim from [TamarinManual, Chapter 3: Initial Example]. A fully commented variant of that example is [TamarinTutorial]. A brief introduction to Tamarin is [MSCB13]. Tamarin's foundations are explained extensively in Simon Meier's PhD dissertation [Meier13]. The bigger picture, i.e. how to formally analyze KE protocols in the Yolev-Dao model using (among others) Tamarin Prover is presented in Benedikt Schmidt's PhD dissertation [Schmidt12]. Both dissertations are more than enough to get you going, but there are a whole lot of additional papers on this subject. Slides from a talk (sadly no video found) by David Basin are also available [Basin18]. Like all provers in the symbolic model, Tamarin too is based on the Dolev-Yao model[DY83].

Tamarin has been used (along with ProVerif and other tools) to verify various drafts of the upcoming TLS 1.3 protocol[TLS13Tamarin].

An introduction to Tamarin is the talk "Tamarin Prover Introduction" by David Wong:

Literature

• [Tamarin] Tamarin Prover (project homepage)
• [TamarinManual] Tamarin-Prover Manual: Security Protocol Analysis in the Symbolic Model
• [TamarinTutorial] Simon Meier, Benedikt Schmidt: Tutorial for the Tamarin Prover for Security Protocol Analysis. September 2012.
• [DY83] Danny Dolev, Andrew C. Yao: On the Security of Public Key Protocols. In: IEEE Transactions on Information Theory, Vol. IT-29, No. 2, March 1983. (full pdf)
• [TLS13Tamarin] Cas Cremers, Marko Horvat, Jonathan Hoyland, Sam Scott, Thyla van der Merwe: Automated Analysis of TLS 1.3 - Symbolic analysis using the Tamarin Prover (project homepage)
• [Schmidt12] Benedikt Schmidt: Formal Analysis of Key Exchange Protocols and Physical Protocols. PhD Dissertation, ETH-Zürich. 2012. (full pdf, doi)
• [Meier13] Simon Meier: Advancing Automated Security Protocol Verification. PhD Dissertation, ETH-Zürich. 2013. (full pdf, doi)
• [MSCB13] Simon Meier, Benedikt Schmidt, Cas Cremers, David Basin: The TAMARIN Prover for the Symbolic Analysis of Security Protocols. In: Sharygina N., Veith H. (eds) Computer Aided Verification. CAV 2013. Lecture Notes in Computer Science, LNCS vol 8044, pp 696-702. Springer, Berlin, Heidelberg. (full pdf via link.springer.com)
• [Basin18] David Basin: Symbolic Verification of Cryptographic Protocols using Tamarin. Summer School on Verification Technology, Systems & Applications. Nancy, France, August 2018. (slides pdf: part 1, part 2, part 3).